COMP4350/8350

Sound and Music Computing

Digital Sound and Synthesis

Dr Charles Martin

Country of the Ngunnawal and Ngambri People

Sound

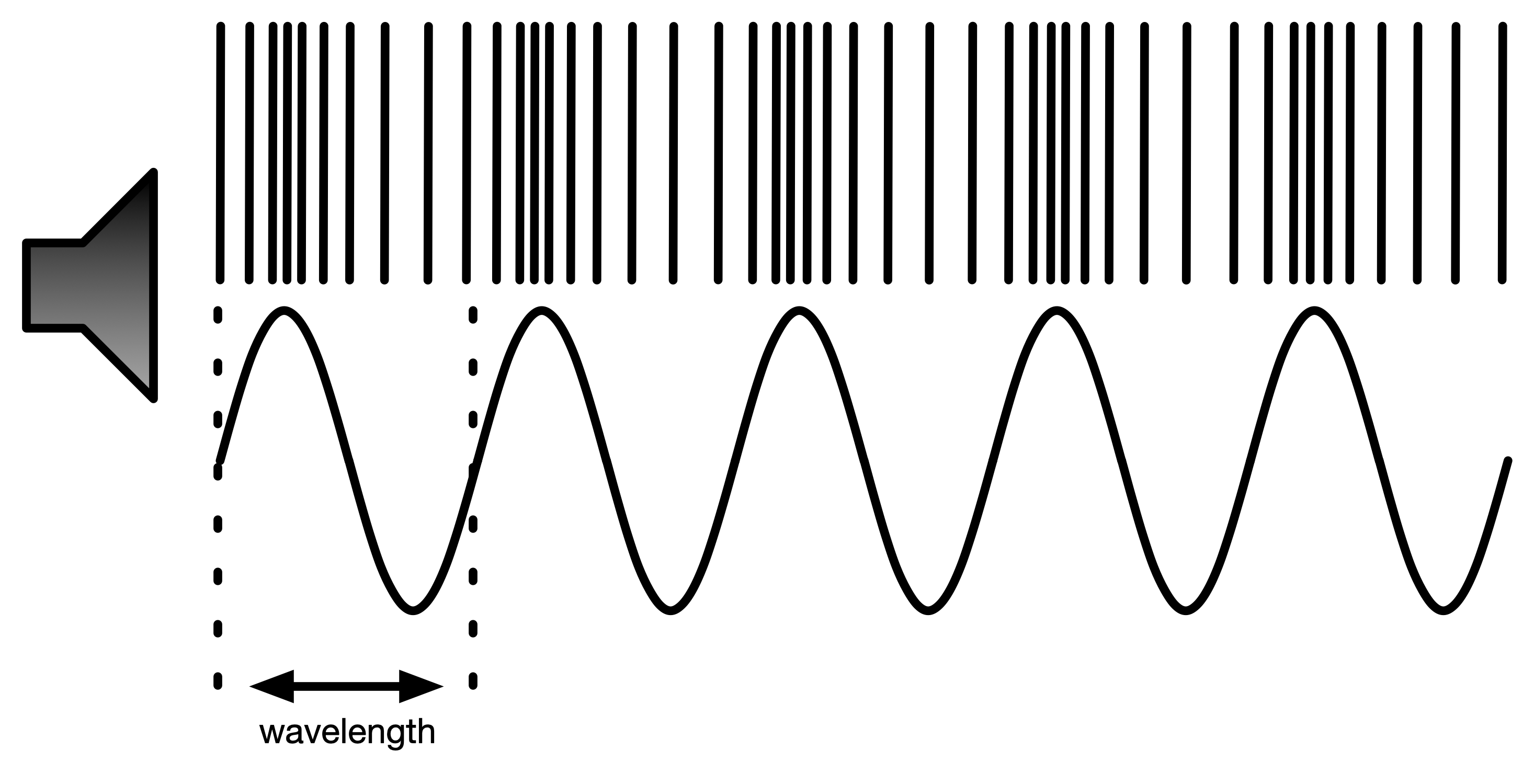
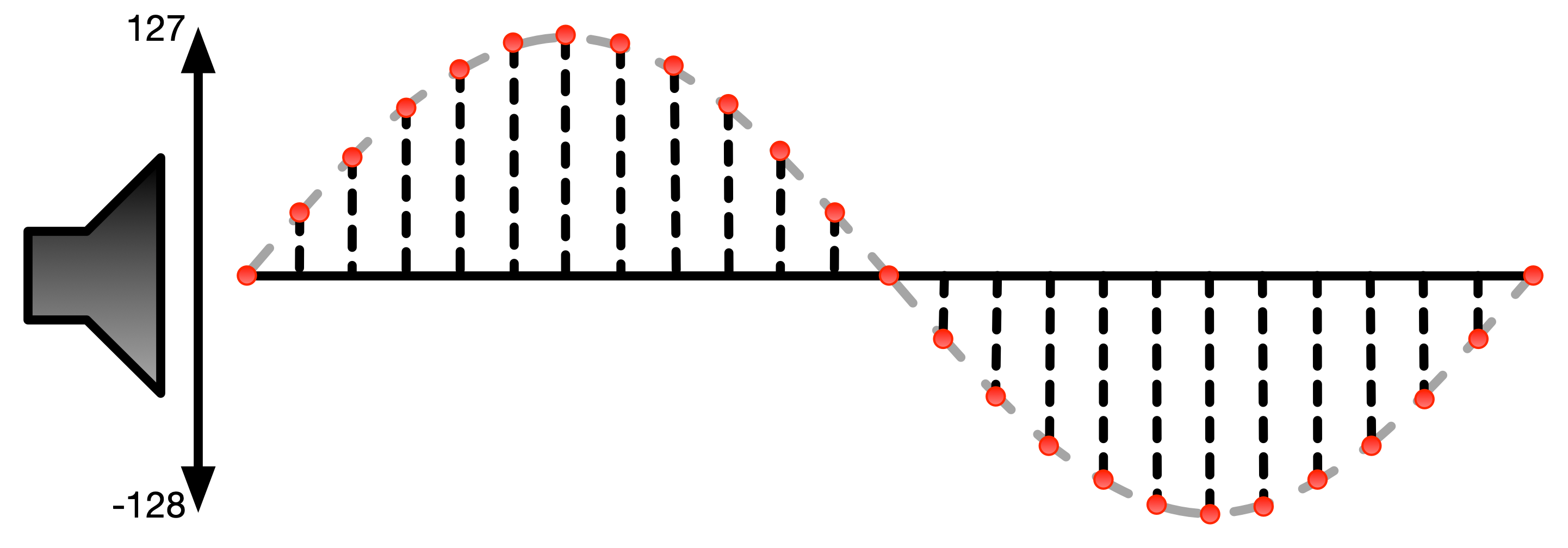
Digital Sound

Why does digital sound work?

Q: How do we get the dots from a regular sound wave (voltage on a wire)

A: An ADC—analogue digital converter—reads the voltage at regular time intervals (sampling rate)

Q: How does the space between the dots get filled in?

A: smoothed out by a DAC—digital analogue converter. Simple way: one part holds the dot value for the sampling rate, next part reacts to changes slowly.

Q: How does the DAC know the right waveform?

A: sampling only works for a limited frequency range. There’s only one right answer up to a certain frequency.

How do we know?

Nyquist-Shannon Theorem:

A signal containing only frequencies lower than B Hz can be (perfectly) reconstructed from samples taken at 2B Hz.

We hear sound up to ~20KHz, therefore most DACs operate a bit above 40Khz: 44.1KHz (standard) or 48KHz (video).

Does this really work?

Yep. Check out these demonstrations:

Unit Generators

Computer music algorithms are usually built from a network of modules that we often call “unit generators”.

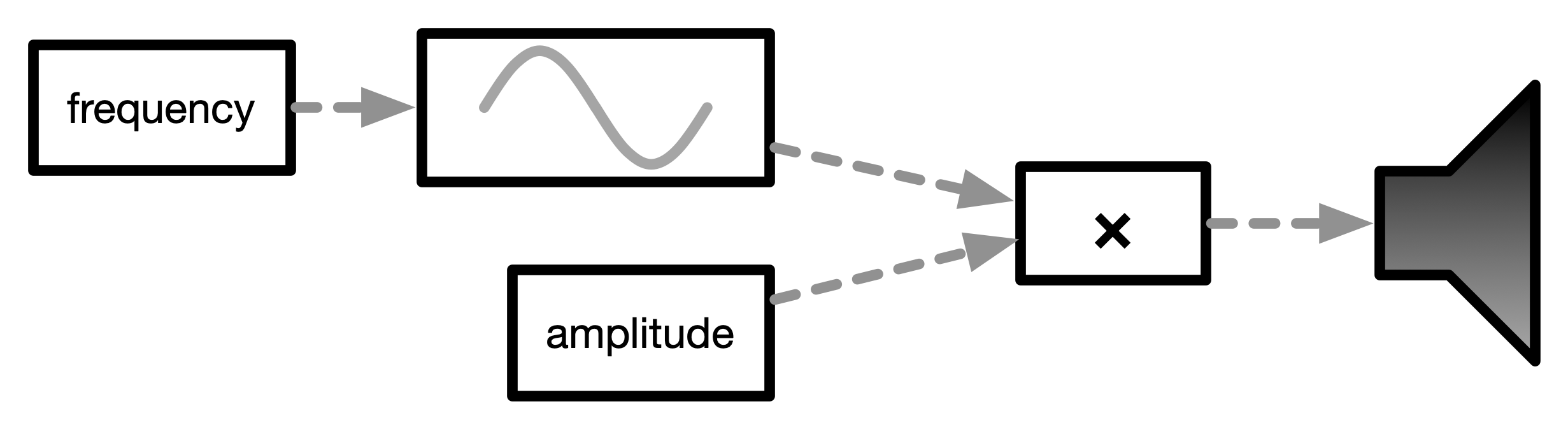
The point here is that sound and music programming involves organising modules so that a signals flow through each part. This can be done with text or graphically.

Pure Data (Pd)

Free tool for making computer music

Developed by Miller Puckette, maintained by MSP and the community (download).

“Old” (circa 1997).

Graphical programming environment.

patching to make sound

Gibber

Free tool for making computer music—in your web browser.

Developed by Charlie Roberts. “New” (circa 2013), under active development.

Start using it at gibber.cc.

coding to make sound

Let’s go do it.

Let’s make a Pd patch. I’ll use the “Put” menu to create an object and type in the object I want: dac~

this is the bit that turns “dots” into sounds… let’s try it.

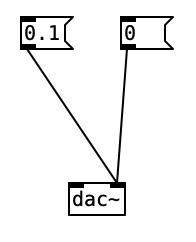
Making a Sound

this is the “hello world” of computer music

osc~ here is a ugen that outputs a cosine wave at the frequency given by its argument.

*~ 0.1 is changing the amplitude to 10% of the maximum.

Change volume with *

Multiplying a sound by a constant changes the volume (amplitude).

For making different kinds of boxes, try the “put” menu, and try the key combinations…

Pd has lots of “things”

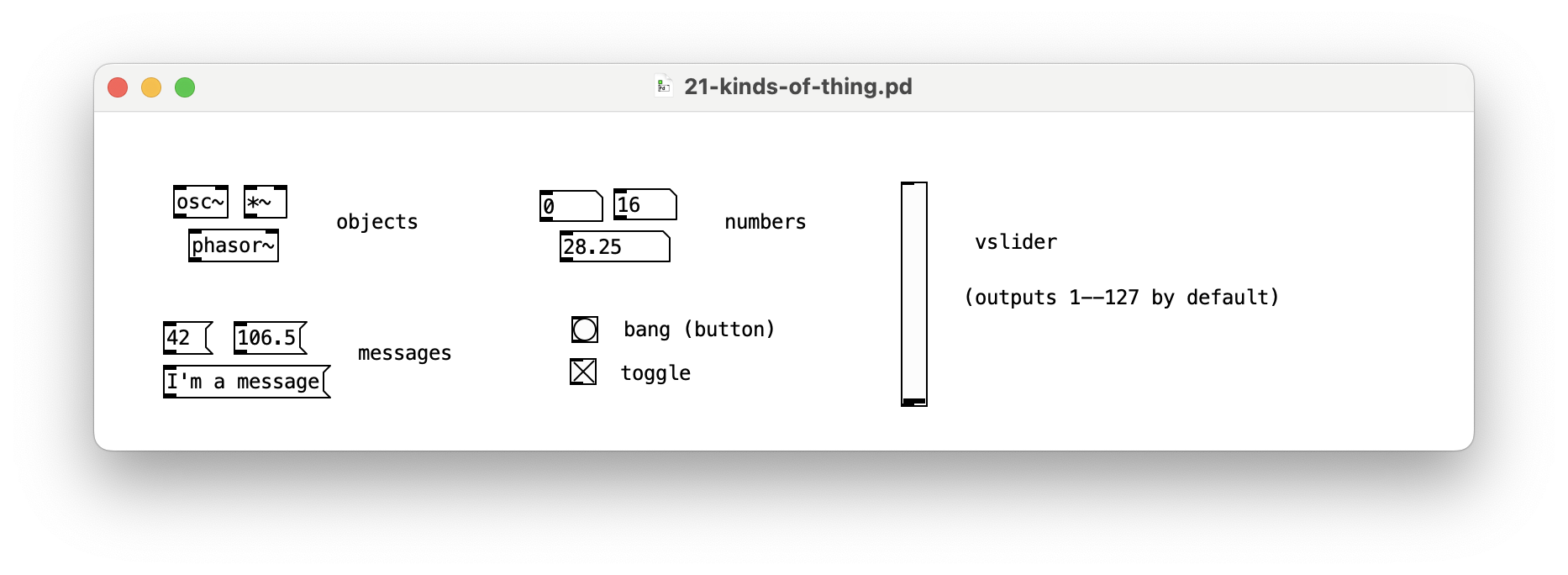
“Objects” are the primary element of programming in Pd, you can find a list of built-in objects in “Help” menu.

Objects with a ~ in the name have audio inputs or outputs.

Try it…

  1. install Pure Data
  2. recreate the sine tone patch
  3. try changing volume with a * and a vertical slider

Do it in code…

Ok, let’s go to gibber.cc/playground and try the same thing:

def = {
  name:'Example',
  type:'Ugen',
  constructor: function() {
    const g = Gibberish.genish
    const graph = g.mul(
      g.cycle( 220 ),
      0.25)
    return graph
  }
}
ExampleSynth = Make( def )
s = ExampleSynth()

s.connect()
s.disconnect()

Why is this more complicated?

“Gibber” is actually the top-level interactive environment / web application.

There are layers below it (different JavaScript libraries) for managing synth definitions and signal processing.

Most of the code on the previous slides was to punch through the layers to get to underlying genish ugens like cycle.

The important bit is: g.mul(g.cycle( 220 ), 0.25)

Try it…

  1. go to https://gibber.cc/playground
  2. clear the sample code
  3. type in the example synth
  4. select all the text and use the Ctrl + Enter key combination to run it.
  5. use the Ctrl + . key combination to stop the sound.

In future we will write key combinations as Ctrl+Enter meaning “hold the control key, then press the enter key, then release both”.

Pd vs Gibber

Pd and Gibber are good at different things (if not, I wouldn’t explain both!)

Pd: nice graphical display of signal flow, easy to experiment with synth design, possible to connect to hardware controllers, bonus built in graphics programming

Gibber: works in a browser, built in collaborative editing, easy to access sequencing and scheduling components.

Additive Synthesis

“Adding” one sound to another is the same as mixing them.

To play two notes at once, just plug both outputs into one input.

Q: How do our brains know there are two sounds even though the waves get mixed together?

Additive Synthesis

We can mix simple sounds to create a complex sound.

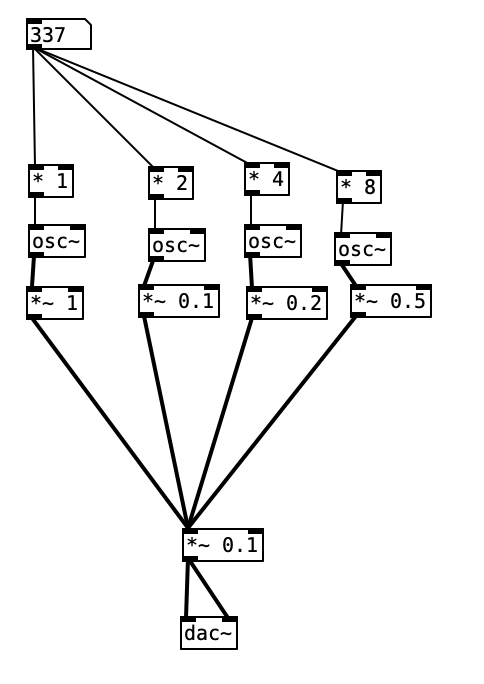
Sound/Music terminology

Pitch: frequency, or how high or low a sound appears to be.

Loudness: amplitude, or how loud or soft a sound is. We also use the term “dynamics”, as in “dynamic range”. In music, this is so important that we use special Italian words (forte, piano, fortissimo, crescendo, diminuendo, a niente, etc).

Timbre: sound colour, klangfarbe, everything else about a sound that isn’t pitch or loudness. Timbre is how you know the difference between bassoon and bagpipes even though they might play the same note.

In general acoustic music, the best way to change timbre is to change instrument. In computer music, this is not true! In computer instruments, timbre possibilities are very wide!

Playing some “notes”

“These frequencies are just sounds. I want to play NOTES”

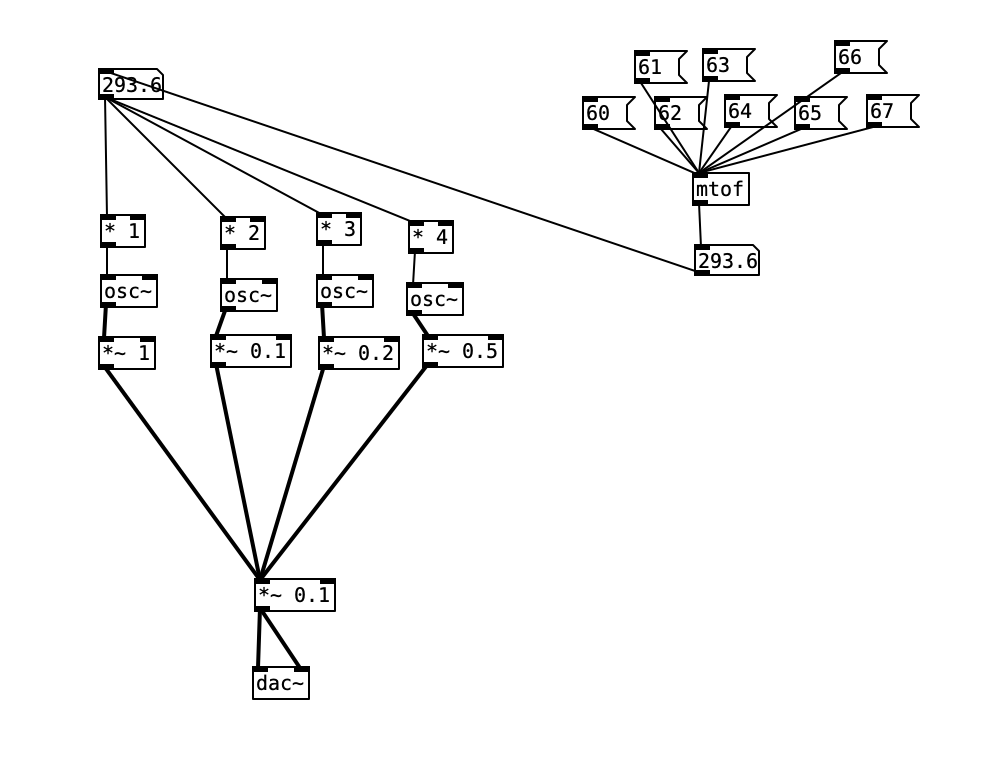
Overtones and Harmonics

  • Generally we call the “lowest” frequency component of a sound the fundamental

  • The others frequency components are overtones

  • Integer multiple of the fundamental are harmonic overtones or just “harmonics”

  • Not-integer multiples are called inharmonic overtones

Consonance and Dissonance in Mixing Sounds

The relationship between frequencies has an important impact on how we perceive sounds.

Adding a frequency multiplied by a simple ratio (e.g., 2, 1.5) provides a consonant sound.

for those musically inclined: x2 is an octave, x3/2 is a perfect fifth, x4/3 is a fourth.

Complicated ratios or multiplication by non-rational numbers leads to dissonant sounds.

e.g., a tritone (augmented fourth) is x45/32

Dissonance isn’t bad!

Inharmonic overtones are a super important part of great sounds like bells, cymbals, triangles, etc (well I am a percussionist…).

Frequency Domain

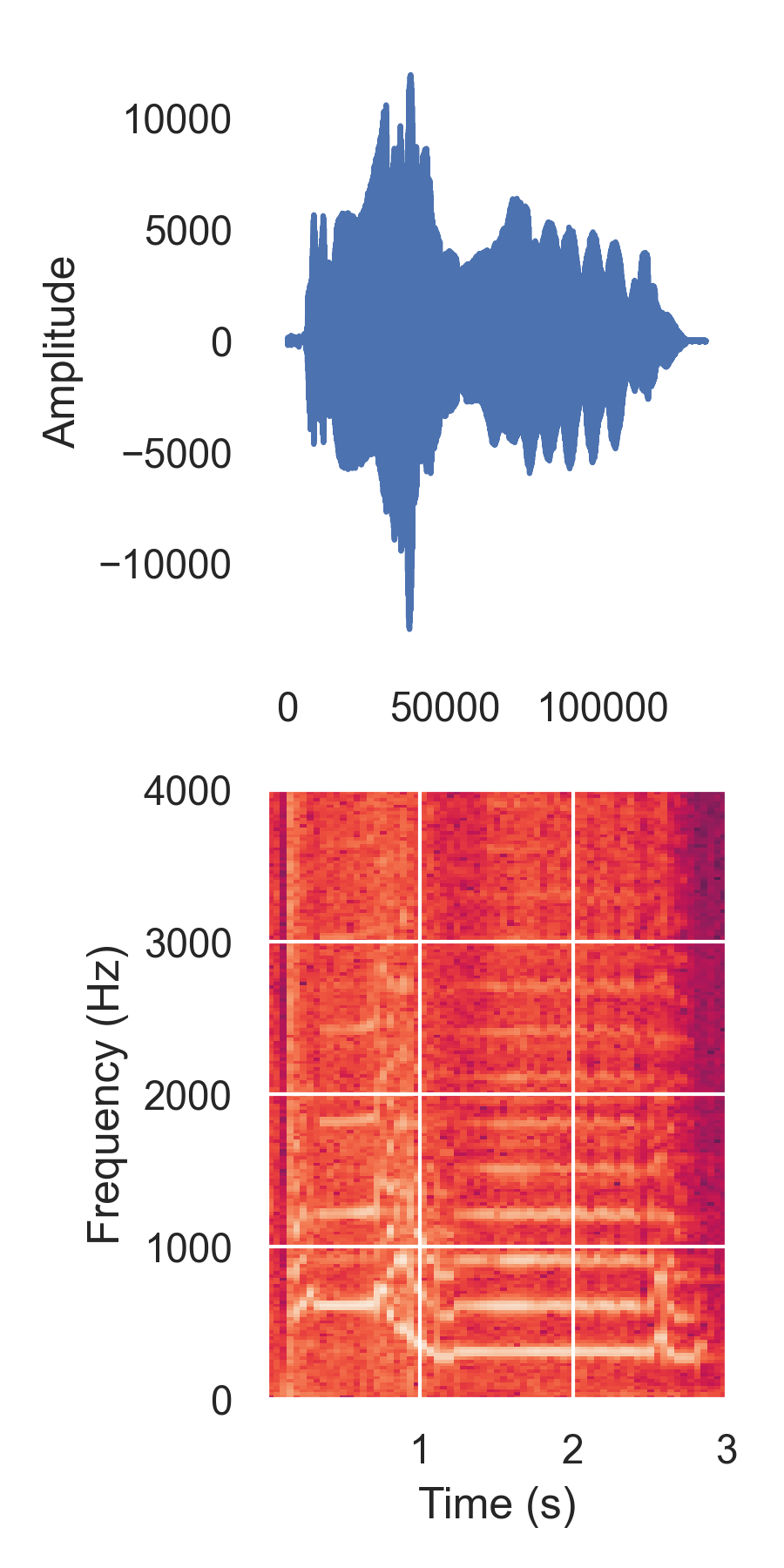
So far, we have represented sounds as a waveform—this is also known as the “time domain” representation.

An alternative representation shows the frequency information (spectrum) in a sound—this is called the “frequency domain” and we can plot it as a spectrogram.

To obtain frequency domain we use a technique called Fourier analysis (more on this later).

try out the Chrome Experiment “Spectrogram”

Waveforms

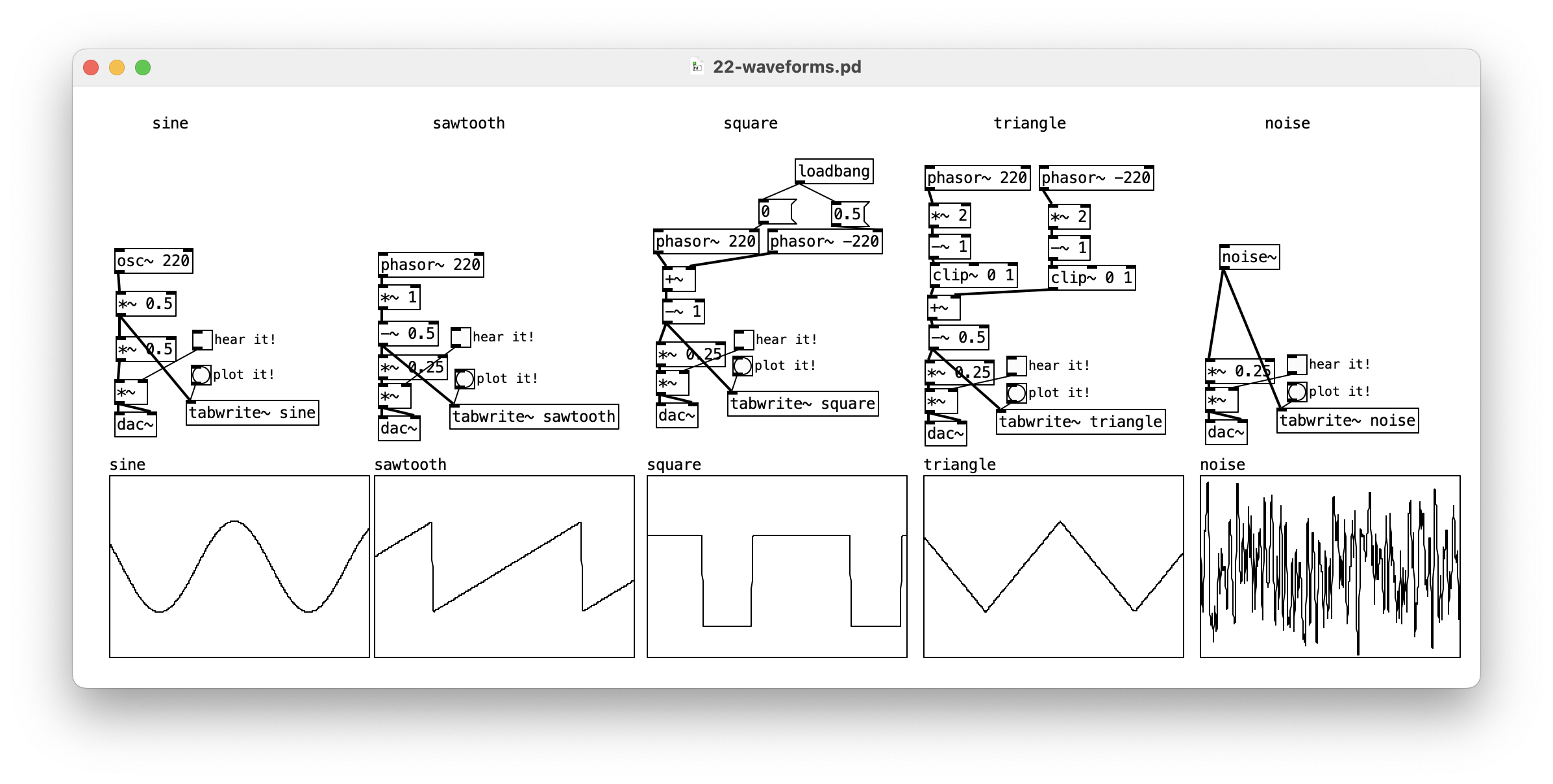
Synthesisers often have different “waveforms” or wave shapes that can provide different timbres. Here are some classics. The “harshness” of these reflects more harmonic overtones.

How does this work?

  • the phasor~ object creates a sawtooth wave between 0 and 1 (half the full range of -1 to 1).

  • phasor~ is usually the start of a signal chain, or for driving other sound making processes.

  • Notice how we used *~ and -~ to scale and centre the waves.

  • clip~ can be used to remove part of a wave

  • if phasor~ has a negative frequency it produces the reverse slope

  • the second input of phasor~ controls phase (what does this do?)

Exercise:

Make an additive synth with a couple of osc~ objects. Try different “multipliers” on the frequency to create interesting sounds!