COMP4350/8350
Sound and Music Computing
Algorithmic Composition
Dr Charles Martin
Composition
You can think of a composition as a program (or instructions) for making sounds.
Compositions is about making choices for what the instructions are.
Choosing is hard!
How do we choose the next sound?

Can we get some help making all these choices?
Music is full of patterns, repetitions, heuristics and systems.
We can take advantage of this knowledge to make algorithms for making insteresting choices.
Algorithmic composition: using a program to make choices for musical parameters (e.g., pitch, rhythm, timbre).
Existed since before computers…
Algocomp: Repetition and Variation
Repetition
- Loops and sequences
- Low frequency operators
- Euclidean patterns
Variation
- Random choices
- Random notes (and making them sound nice)
- Controlled randomness
- Markov processes
Low frequency oscillators
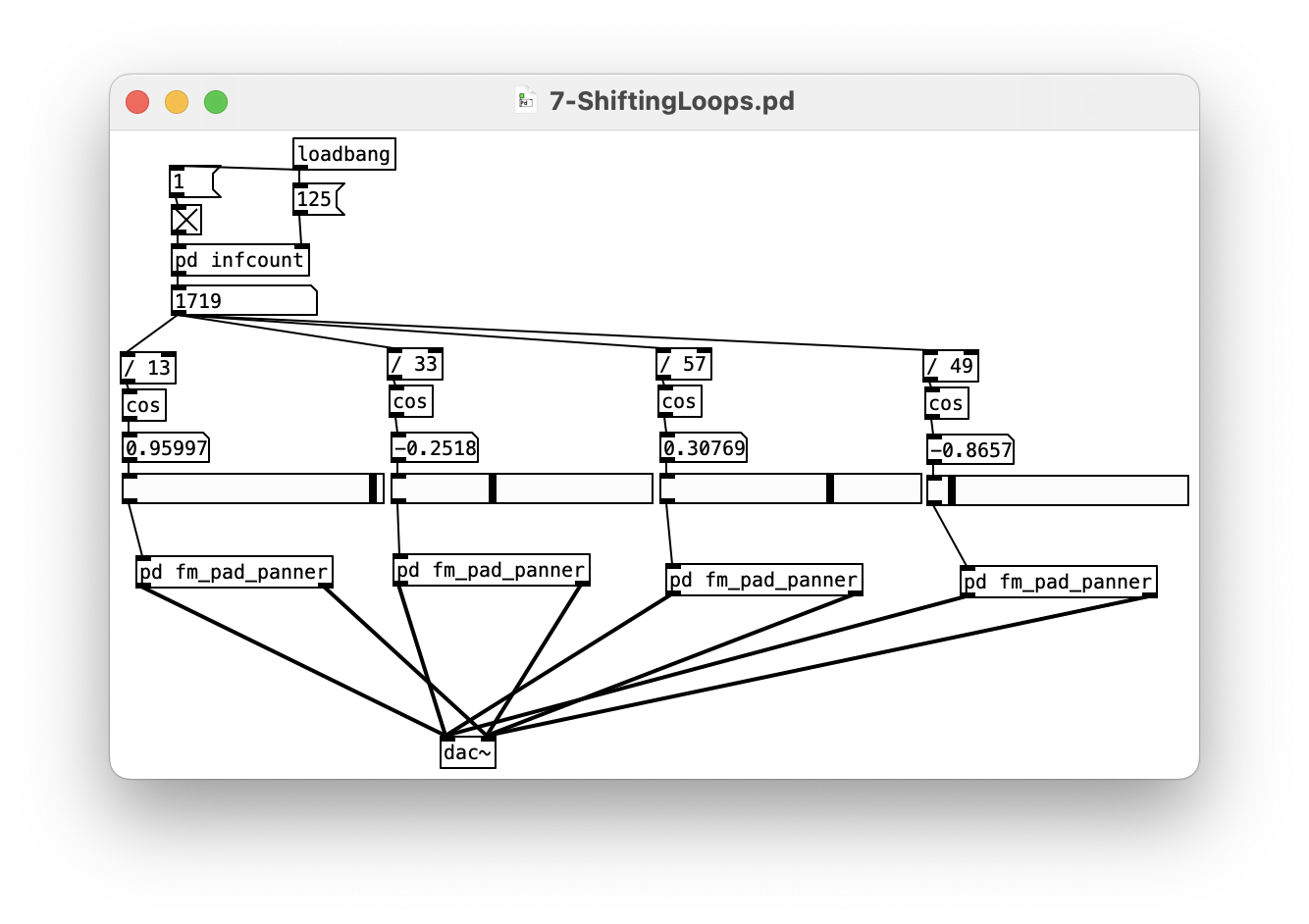
Counters and cos, a quick LFO.
These are useful for non-pitch parameters:
- velocity
- filter cutoff frequency
- speed of grain playback
Try randomising LFO speeds or controlling the LFO with an LFO.
Euclidean patterns
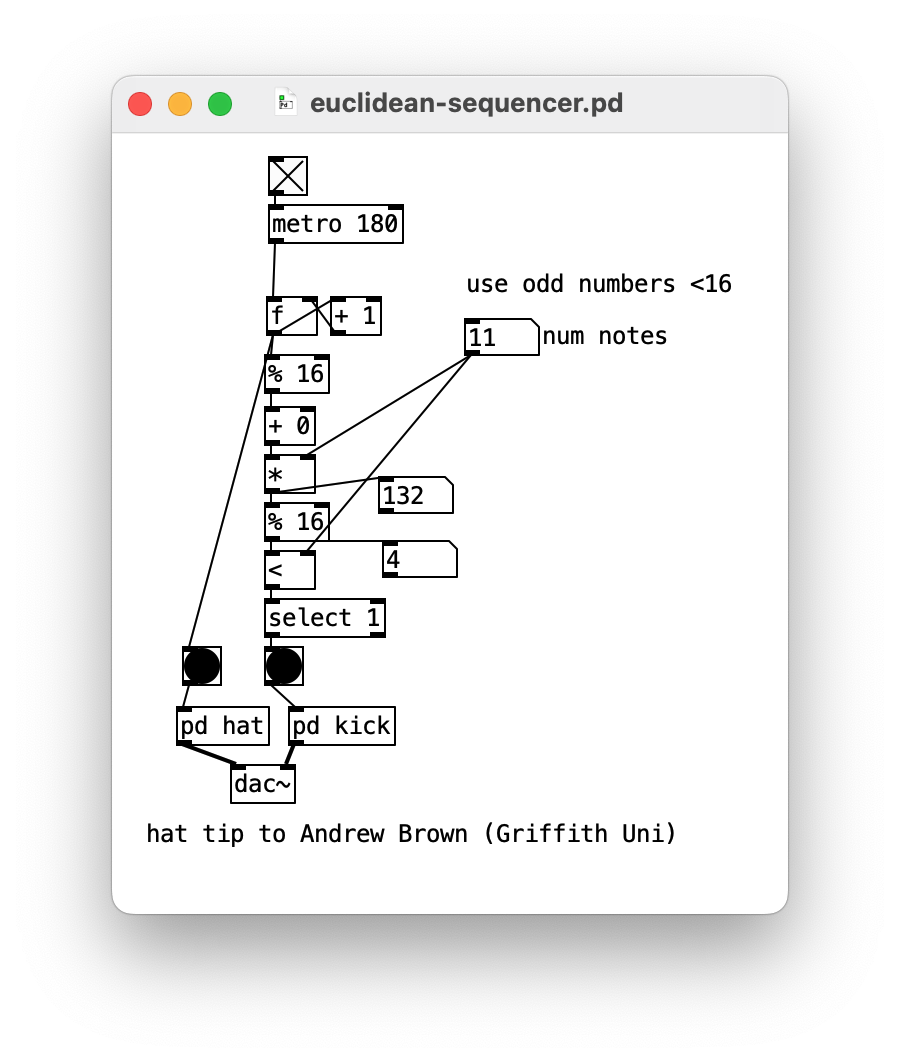
Eurodance in a box: Algorithm to space notes evenly in a sequence of fixed duration spaces.
Produces common and useful patterns, e.g., clave patterns, that sound great in EDM and are used all the time.
- watch Andrew Brown’s video
- try odd numbers less than the number of steps (e.g., 5, 7, 9, 11, 13…)
Variation
We’ve touched on random previously, now we’re going to process random values in difference ways:
- Frequency
- Pitches
- Scale degrees
- Chords
- Sample points
Random Numbers
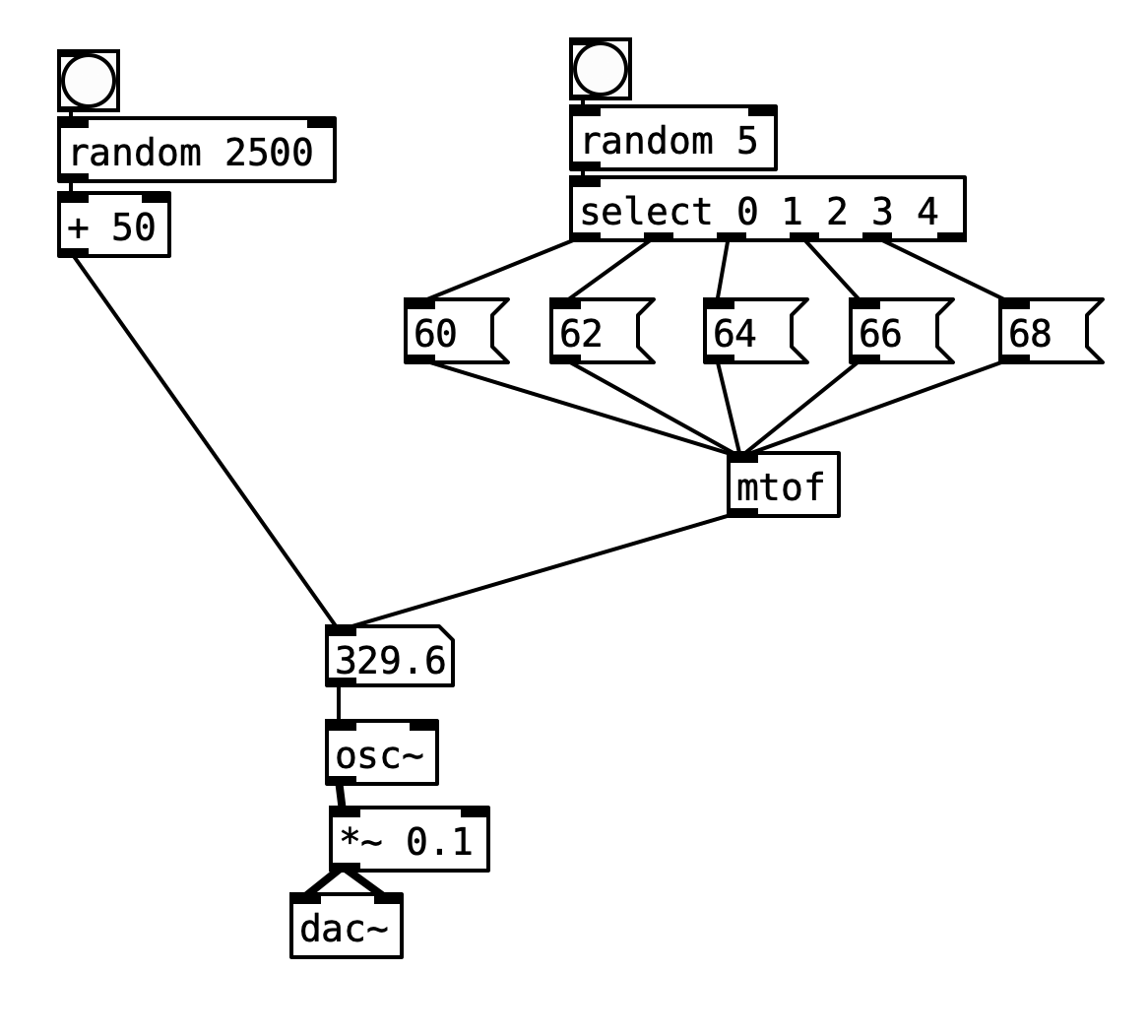
you can use random numbers to create frequencies for a synth.
Pd really only has one kind of random function: integers between 0 and $1 (the first
argument)
want to trigger different things randomly? try select
Random sequences
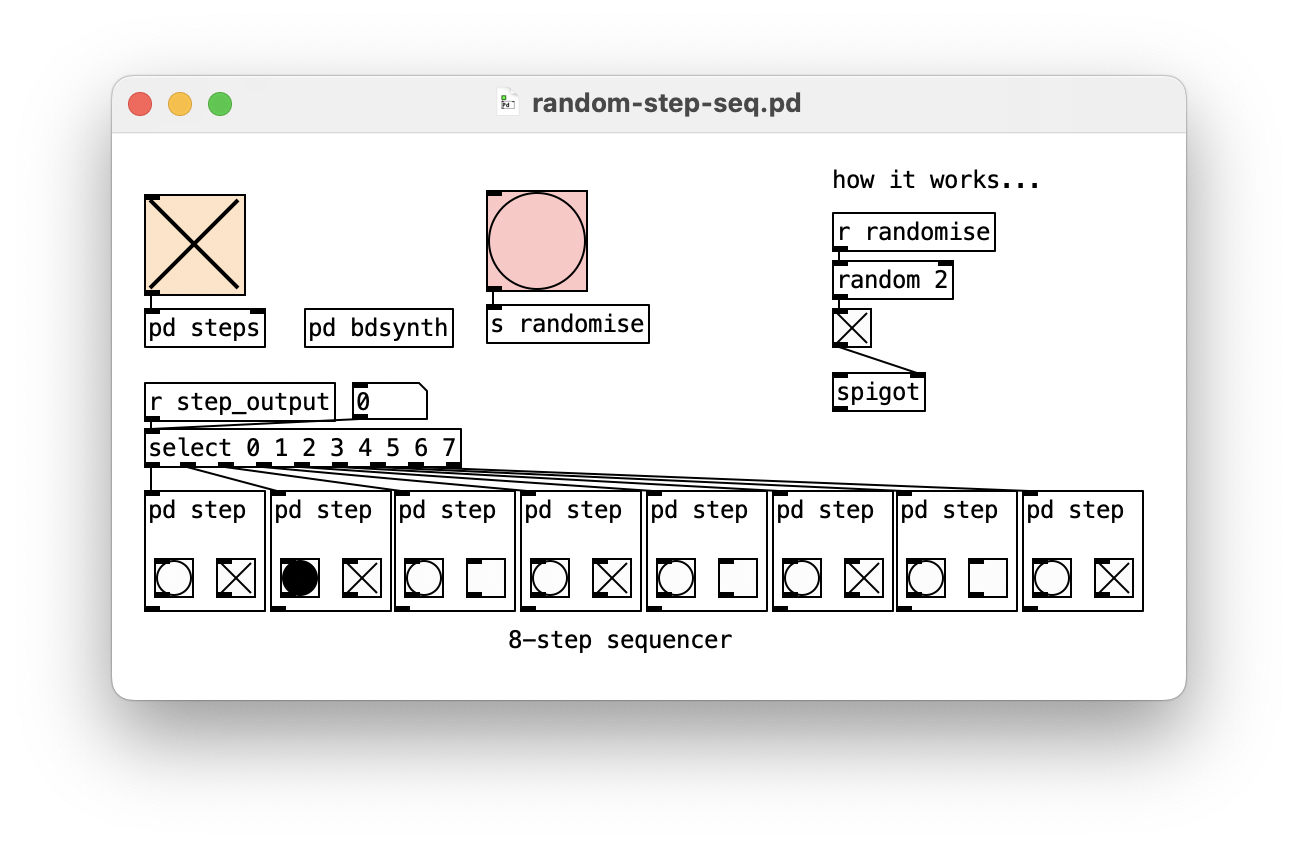
Try using random to control the steps of a sequencer.
- use
random 2to create either a 0 or 1 - use this value to update a
spigot
Good for making quick, interesting patterns!
My hardware drum machine has this feature!
Frequencies to Pitches
Recall that different multiplying frequencies produces consonant (nice-sounding) intervals.
Doubling a frequency results in a frequency that we call an octave.
Pitches (A, B, C, D,.. etc) are distributed along the frequencies so that the ratio between any two adjacent pitches is the same.
We end up with pitches that sound even and logarithmic scale of frequencies.
To convert, use mtof or ftom in Pd or look at this table.
In Pd, we use MIDI numbers, not note names. 60 == C4, 61 == C#4, etc…
12-Tone Equal Temperament
In European and Chinese music (among others) we tend to divide the octave into 12 pitches with a ratio of $2^\frac{1}{12}$ between the frequencies.
You can call this “12-TET” (12-tone equal temperament).
Other schemes are possible, used in practice and sound super cool, e.g.:
- $n$-TET for different numbers
- just intonation that uses only simple ratios
- other non-equal temperaments (sounds super cool)
Random MIDI Pitches
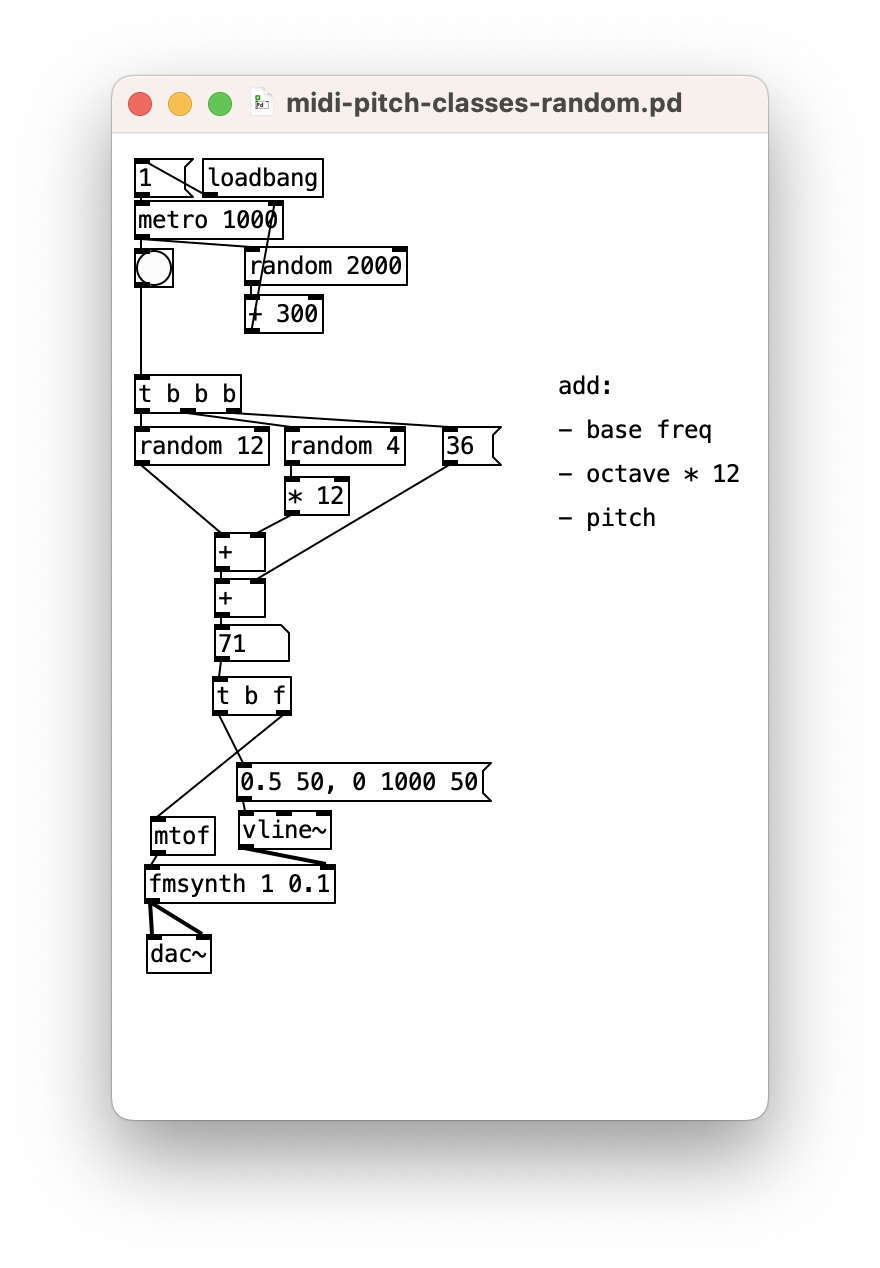
Using the same random object, but with different values, we can create MIDI pitch numbers (0-127).
You might want to use a nice “musical” range, e.g.,
- from 36 (2 octaves below middle C)
- to 84 (2 octaves above middle C)
Let’s abstract things a bit by using two random choices one to choose pitch, one for octave. We can separate out a nice parameter for the base pitch.
Rhythms with metro
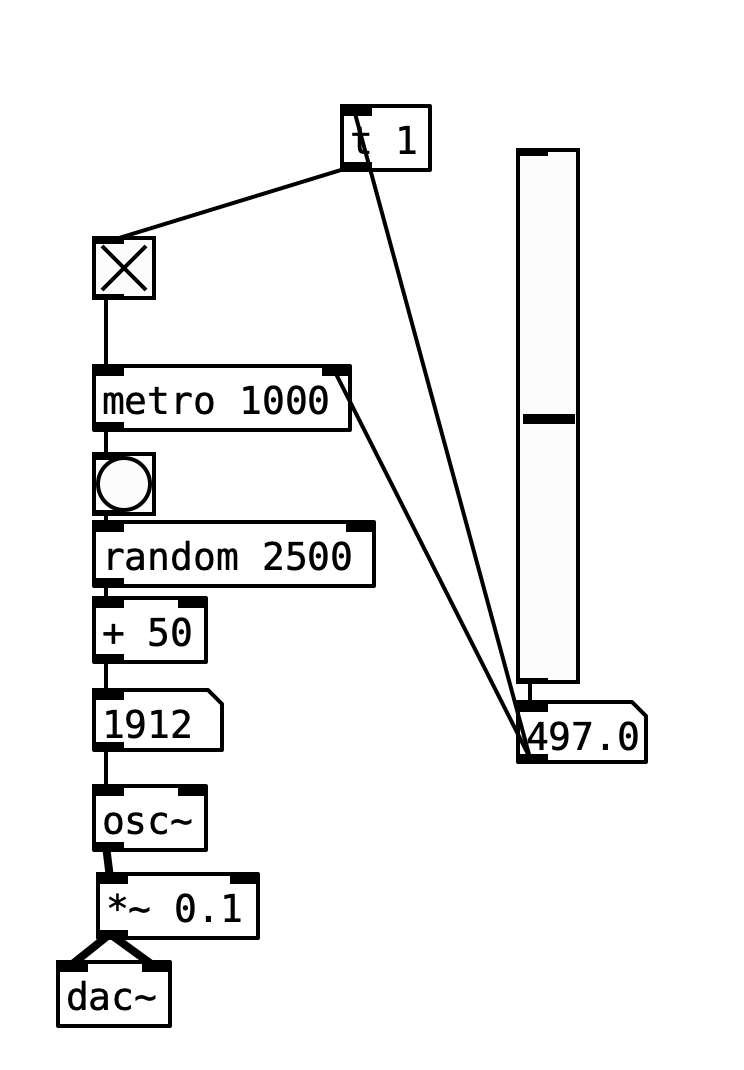
You know how to schedule repeating notes with metro
you have to supply the number of milliseconds in between bangs.
Random rhythms
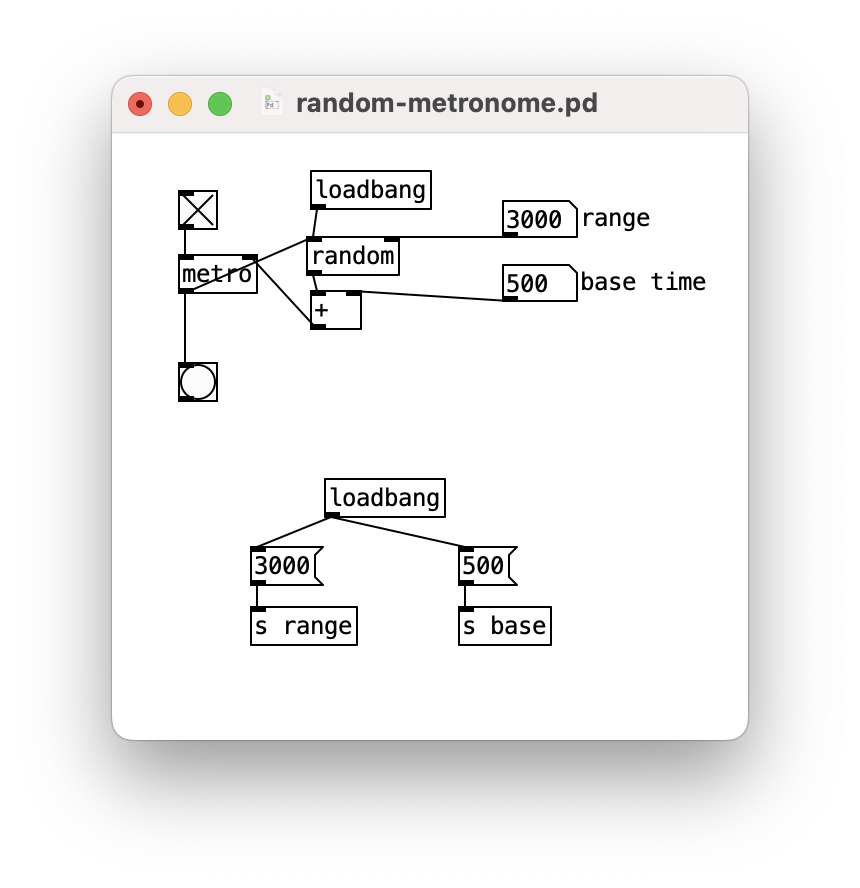
How about randomising the metro’s time after each bang?
We can make a “random” metronome with a maximum and minimum time.
Making a composition with random metro
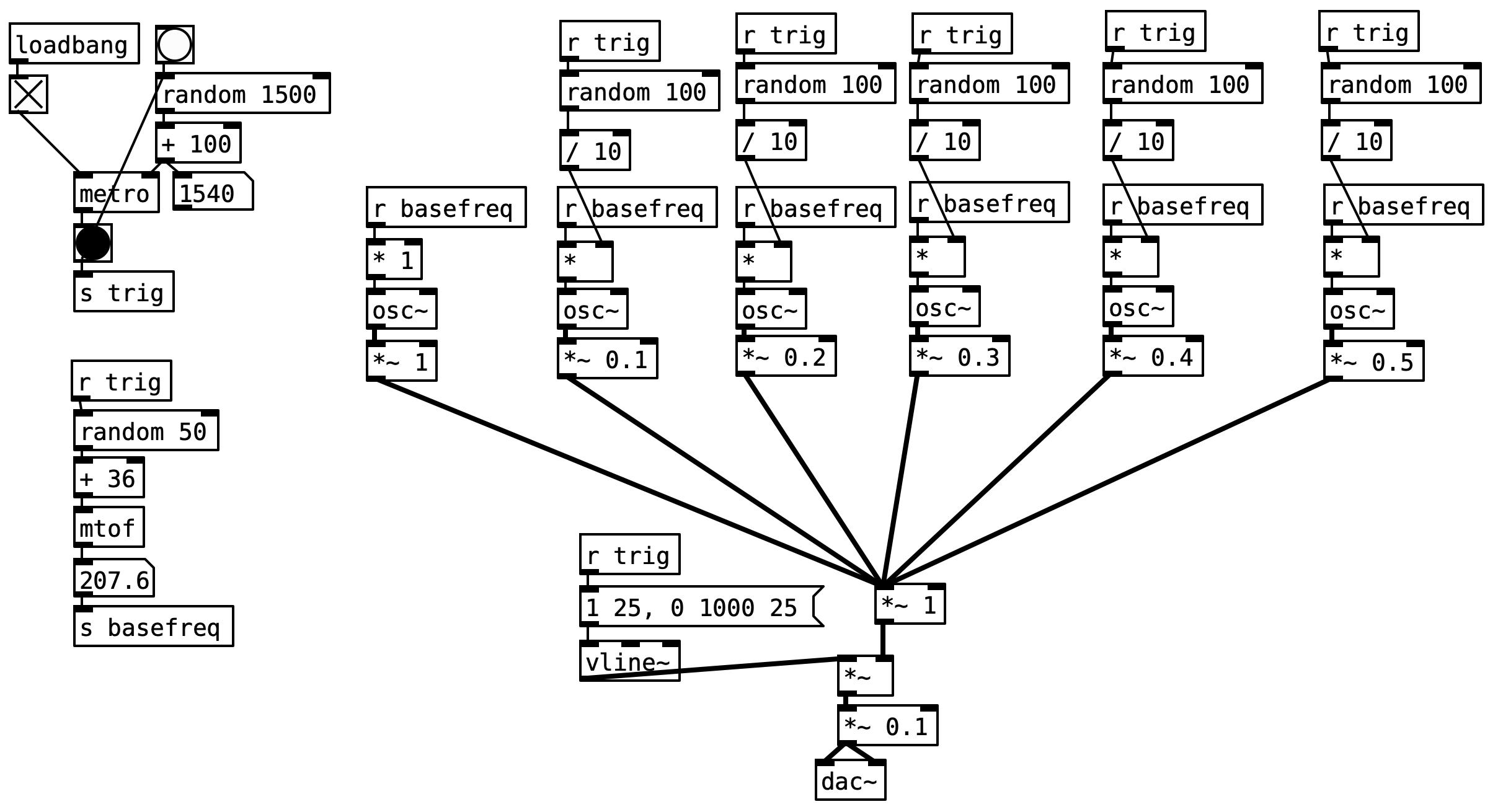
This composition uses additive synthesis to create:
- random pitched notes
- random (inharmonic timbre)
- at random times!
It’s random all the way down.
From Frequencies to Scales
Using all the frequencies can sound good.
Can also be good to restrict to particular collections of pitches.
This can let us:
- reinforce the idea of a “central”, “home”, or “root” pitch
- create a sense of movement by moving away from home and then coming back again
Using pitch collections
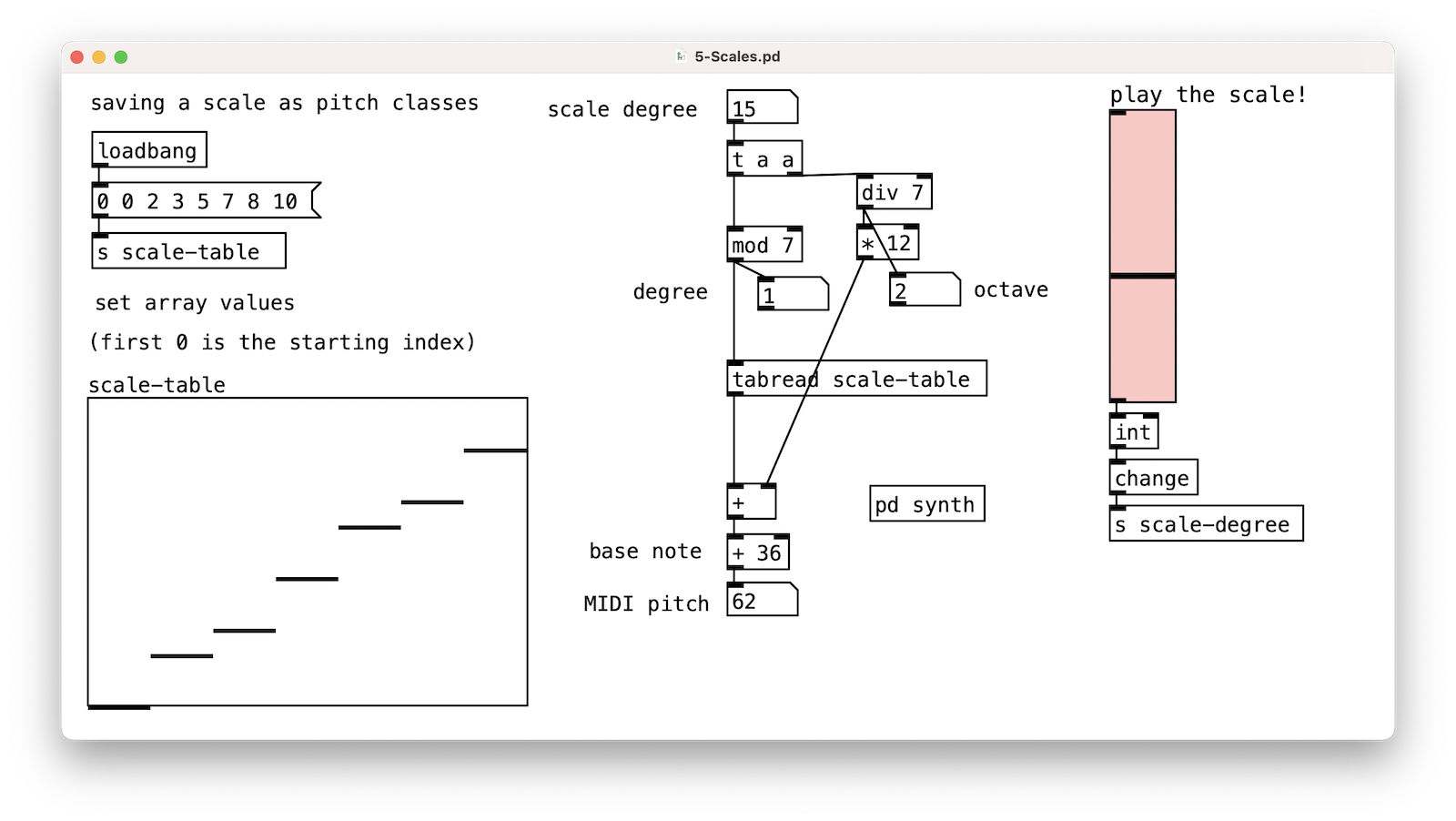
It can sound nice to use a subset of the 12 pitches.
We can select the same subset in each octave.
In music we call this a scale.
You can define a scale as an array showing the offsets from a starting point.
Then use tabread to access the offset and add it to a starting MIDI note.
Popular scales
We’ve travelled deep music theory land, no turning back now.
Scales can have different numbers of notes, you might have learned some 7-note, heptatonic scales and are probably familiar with the sound of 5-note pentatonic scales.
Here’s a few examples of scales:
- minor pentatonic:
[0, 2, 3, 7, 8] - whole tone (hexatonic):
[0, 2, 4, 6, 8, 10] - dorian (heptatonic):
[0, 2, 3, 5, 7, 9, 10] - whole/half octatonic:
[0, 2, 3, 5, 6, 8, 9, 11]
Scales have lots of interesting patterns and properties but we won’t go into further detail.
Scale objects
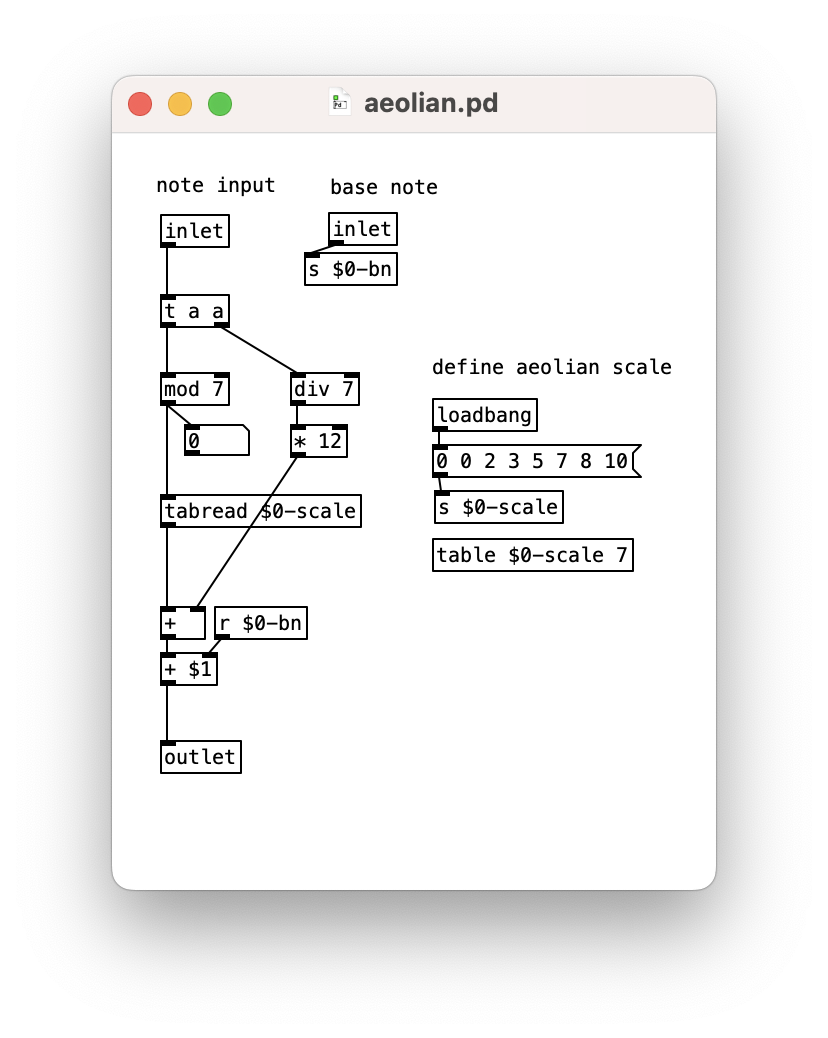
Pd doesn’t have any built in knowledge about scales.
It’s straightforward to create objects for scales you might want to use, see the aeolian.pd as an example.
- This is a good time to create re-useable abstractions in separate files.
- If you wanted to compose with a certain scale (e.g., the lydian dominant mode), you might want to generate notes in different parts of your patch.
Composing with scales
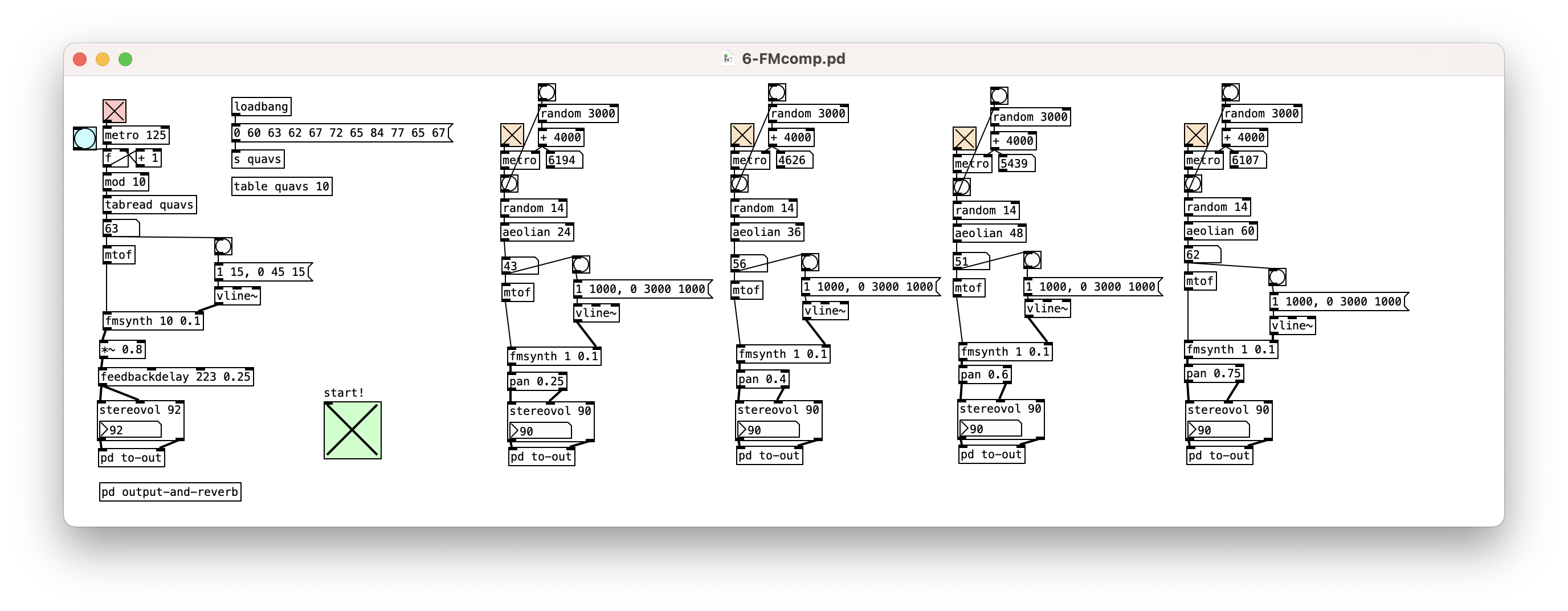
Here’s an example with aeolian generating FM pad sounds.
Go do it: make a composition with a scale
Copy 5-Scales.pd from the board and use it as the basis for a composition.
- set up a table to store the notes
- add the notes to the table
- make a sequencer
- read out the notes one by one and use them to play a synth
Harmony
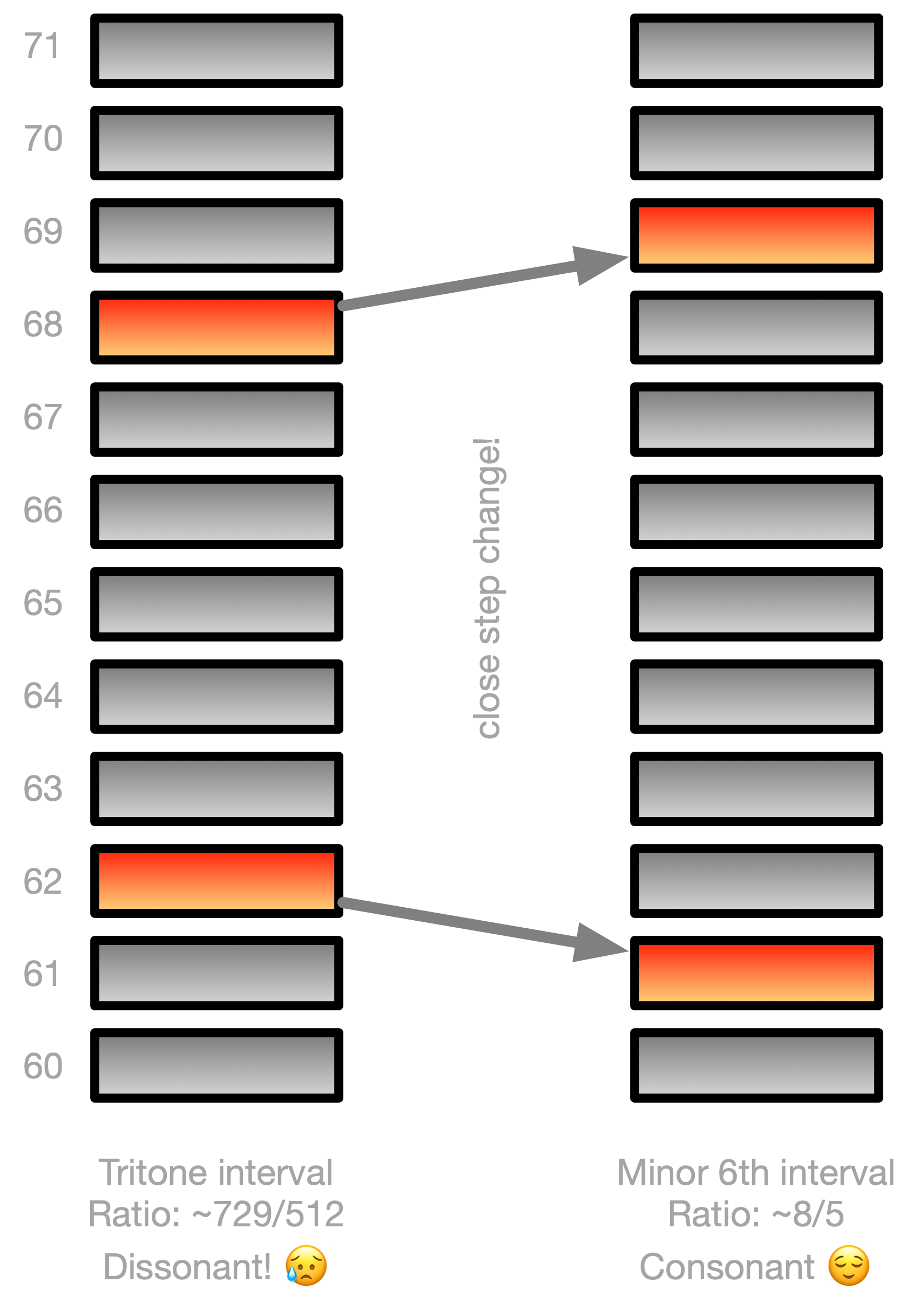
We’ve talked about consonant and dissonant combinations of frequencies before.
This idea can explain why melodies seem move away and then come back “home” to a certain pitch.
Movement from dissonant to consonant gives us a sense of “movement”.
Structured changes between combinations of frequencies is called harmony. It’s a deep study but we can look at some useful basics.
Root notes
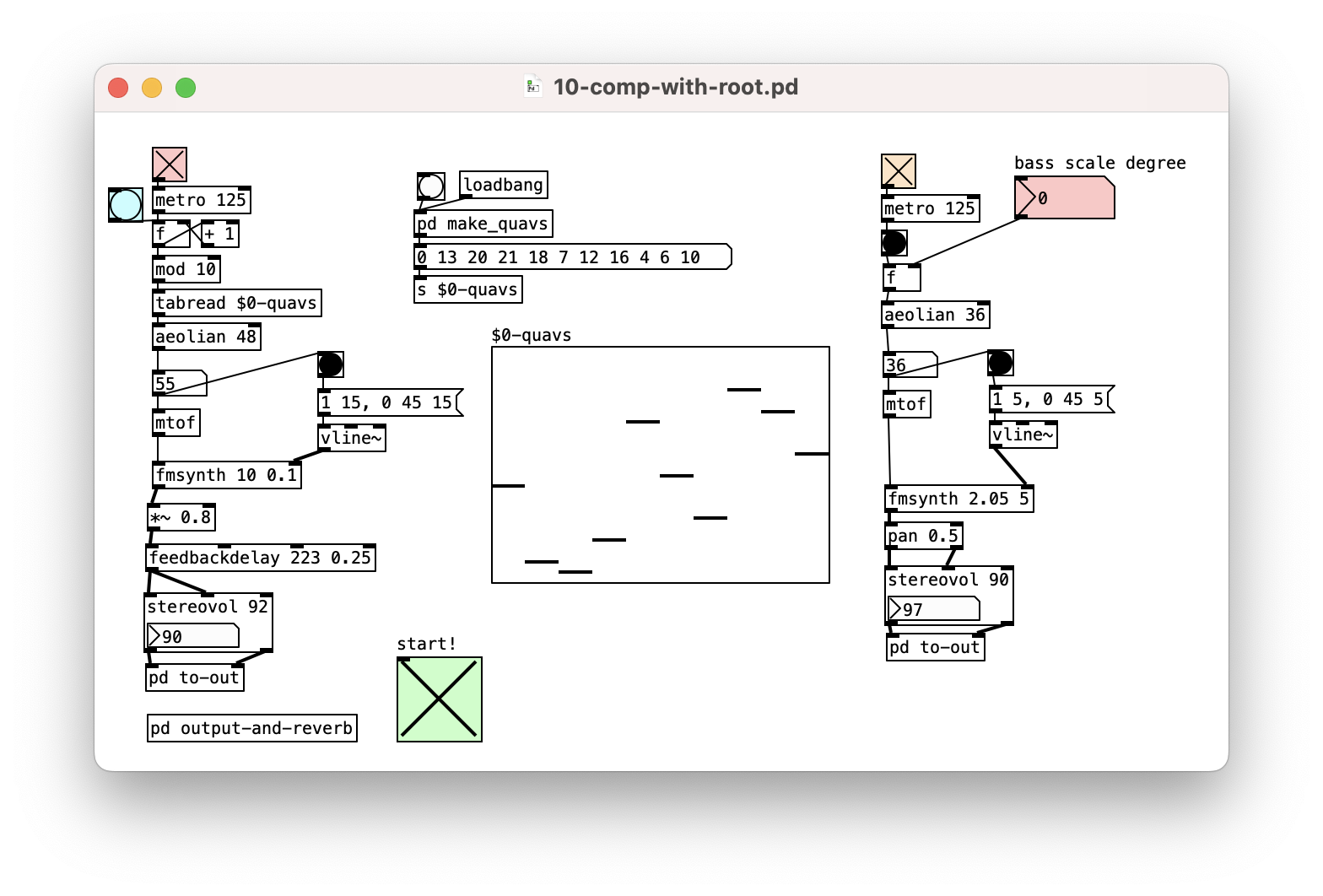
Now that we understand scales, we can call the first note of a scale the “root”.
It’s often where we start a melody and where we return. (not always!!)
You can emphasise a scale by using the root note as a second part (e.g., a repeating bass line, like in techno)
Chords from a scale
The other notes (or degrees) from a scale can be used for a bass line as well. E.g.,
- create a repeating sequence from a scale
- play repeating bass line with scale degree
[1, 2, 6, 5]
This changes how we hear the original sequence!
Changing the bass note makes us hear that note as the “new” root, and we hear the sequence differently.
Chord symbols and numbers
Harmony is complicated and there are lots of ways of notating and explaining harmonic changes.
- We can define a chord to be a collection notes played together (e.g., on a polyphonic synth).
- The root note is the lowest note in the chord.
- Many people use Roman numerals for chords. The numeral matches the scale degree that the chord comes from.
- We use capital letters for a major chord, lower case for minor (and other symbols for… extra details)
So our chord progression [1, 2, 6, 5] on a major scale would be: I, ii, vi, V (the major/minor-ness is taken from the notes of the scale here)
Composition with Bass and Chords
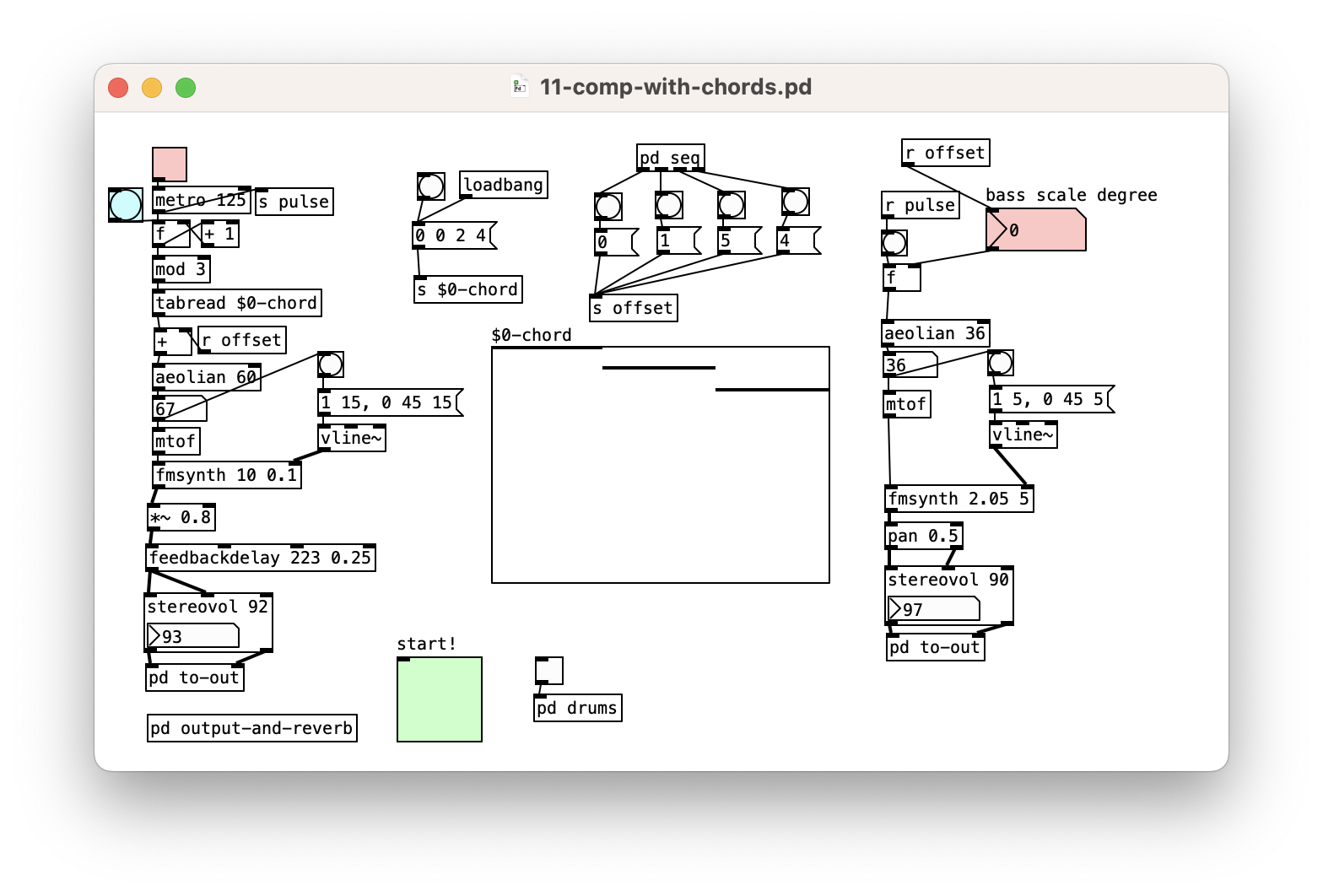
Here’s something simple:
- first chord: notes
[1, 3, 5]from the scale - other chords: same spacing, transposed up
- progression is
[1, 2, 6, 5] - LH synth: chord notes in sequence (arpeggio)
- RH synth: root note bass
- sequencer moves forward through the chords
just add drums and we have techno!
Decisions and directions
Our decisions have, so far been low level: “I want to play a note, but which one?”
What about some higher level decision making:
- moving through sections
- playing or avoiding notes
Controlled randomness
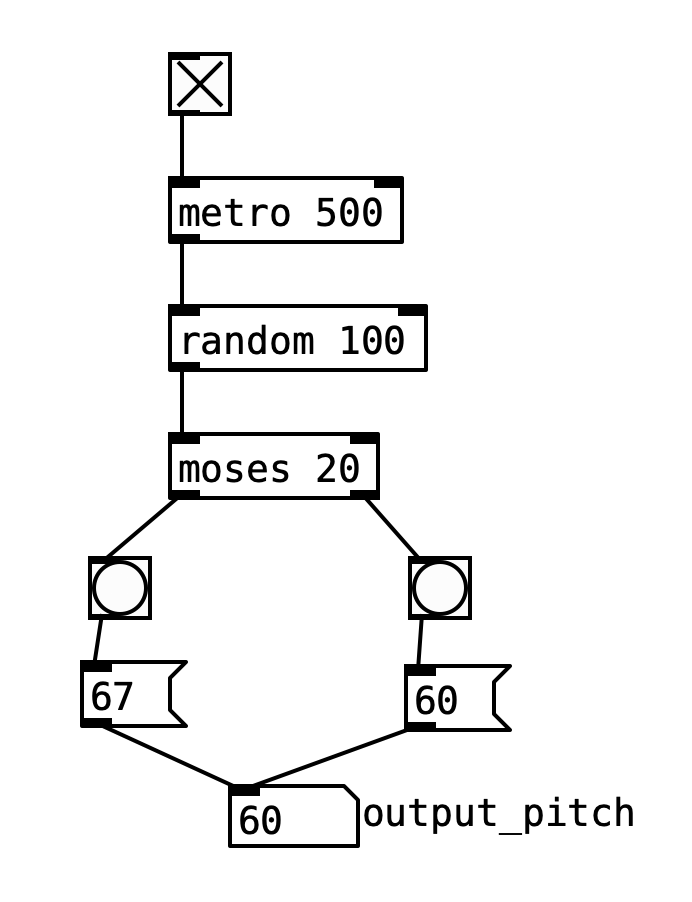
Suppose you want to take one action 20% of the time, and another 80% of the time?
You can split random numbers with the moses object to achieve this.
This extends to more weighted decisions if you want.
Probabalistic sequencer
Try using a probability instead of a toggle on each step of a sequencer.
My hardware synth and drum machine have this feature!
Markov Process
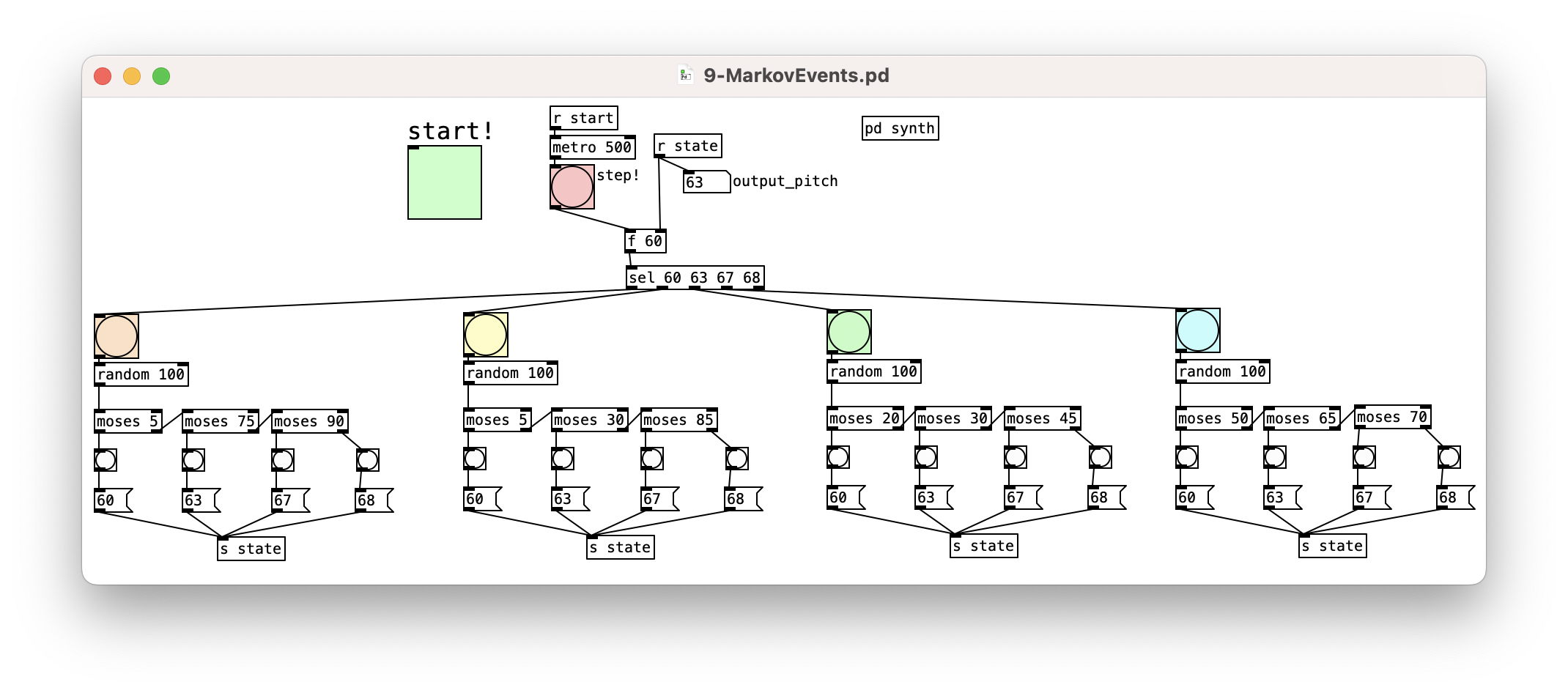
What about having a different weighted decision depending on what the last decision was?
This is called a Markov process. You can do it with the moses method, but it
might get out of hand quickly.
Maybe try c_markov.pd in rjlib.
Fader jam

Go do it: make an algorithmic composition
Get started, you have to make something today that includes:
- synths.
- randomness.
- high-level controls.
Want some extra tools?