INTRODUCTION TO Haskell
This document works you through all the Haskell code used in lectures and tutorials, explaining how to read and understand the code provided.
Before we jump into the code from lectures, let’s run through a simple example. Let’s try to write a code to calculate the sum of three integers. Haskell functions are like functions in math, so we can start there, how would you write this function in math,
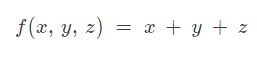 .
.
Here, we specify the variables within parentheses, in contrast Haskell identifies the separation of variables with spaces. So we can write the same function using Haskell as f x y z = x + y + z.
Additionally, we need to specify the type signature of the function. In Haskell we use :: to do this. For example, if we have function:: Int -> Bool this tells the compiler that there is a function called function of type Int -> Bool.
All Haskell functions take an arbitrary number of inputs and return a single output. This is denoted in the type signature. Each input and output is separated with -> sign. For example, function:: Int -> Bool says that “function” is a function that takes an Int as input and returns a Bool as output.
With this let’s go back to write the function f. We know that f takes in three Int s and gives an Int as output, hence we can write the type signature of the function as f:: Int -> Int -> Int -> Int where the first three Int denote the inputs and the last one denotes the output.
Putting it all together, we get :
f:: Int -> Int -> Int -> Int
f x y z = x + y + z
We wrote our first Haskell function!!!
Let’s see what would happen if we run f(3,4,5), in this case the variable x takes the value 3, y takes the value 4 and z takes the value 5. Using this Haskell will evaluate x+y+z which would be 3+4+5 and return 12.
For this course we only require an understanding of the syntax to be able to understand and interpret code, from here on I explaine code that was provided both in lectures and in practicals. For each bit of code, I will start off by mentioning the reference to the lecture or practical and the page it’s found (with a link that can be clicked on), then provide the code and guide you through understanding the code.
Let’s start with lecture code, First Order Logic page 30
sfz :: Int -> Int
sfz 0 = 0
sfz n = n + sfz (n-1)
Applying the concepts taught above, we know the type signature of this code. sfz :: Int -> Int says that “sfz” is a function that takes an Int as an input and returns an Int as an output. The lines after the signature show the function definition: what the function does. sfz 0 = 0 says that if 0 is passed as an argument to the function “sfz” then the output would be 0. sfz n = n + sfz (n-1) says that if n is provided as input, then the output is n + sfz (n-1).
A few things to note regarding this, when numerous definitions of the function are given, Haskell will execute it from top to bottom. Hence, if we are calling sfz 0 it would always execute the first line and not the second.
First Order Logic page 35
sumodd :: Int -> Int
sumodd 0 = 0
sumodd n = (2 * n - 1) + sumodd (n-1)
Using what you have learnt so far, try to identify what this syntax says.
This can be interpreted in the same way as above. sumodd is a function that takes an Int and returns an Int. If given 0, the function will return 0, else for any other value n it will return the value (2 * n - 1) + sumodd (n-1).
FUN FACT! Both these are recursive functions, as the function is called within the function definition.
( The same concept can be used to understand functions ta and tb defined later on in the same slide.)
Function composition#
Note that the notation \(\cdot\) has been used in numerous exercises and past papers, this denotes composite functions. If we consider the example \(f \cdot g \ x\) , this can be written mathematically as \(f(g \ x)\). In other words \(f \cdot g\) is a new function that takes the output of \(g\) and provides it as input to \(f\). Let’s work through a simple example, consider the two functions:
add1:: Int -> Int
add1 x = x+1
multiply5:: Int -> Int
multiply5 x = 5*x
It is clear that the functionadd1 adds one to the input, and the function multiply5 multiplies the input by 5.
Now if we consider multiply5 \(\cdot\) add1 this is a function that takes an int as input and returns an int as output.
Hence if we run multiply5 . add1 8 this is the same as computing multiply5 (add1 8) = multiply5 (8+1) = multiply5 9= 45.
Now moving on to the lectures on structural induction, here you come across the concepts of lists and trees. Let’s start off by understanding what these two data types are.
Lists#
Lists in Haskell are just like the lists you find in the real world. Any list in Haskell has a particular type, for instance, [Int] that denotes a list of Ints. Here all the elements must be of Int type. A list is written within [] where each term is separated by commas. For example, a list of 1,2,3 and 4 would look like [1,2,3,4]. And an empty list would be [].
This can be shown by:
data [ a ] = [] | a : [ a ]
There are two main functions that are used with lists,
-
:, this takes in an element and a list and adds the element to the start of the list,example :
1 : [2,3,4] = [1,2,3,4] -
++This takes two lists and returns a single list and concaternates them.Example:
[1,2,3] ++ [4] = [1,2,3,4]
A list can be defined either as an empty list denoted by [] or as an element added onto another list (empty or not) which can be represented as x:xs, where x denotes the first element and xs denotes the rest of the list.
In other words, any list that is not empty can be represented in the form x:xs.
For example a list of one element can be denoted in the above notation as x:[], where x takes the value of the element. A list of two elements can be written as an element added onto a list which already has an element x:y:[] which is the same as [x,y], where x denotes the first element of the list and y denotes the second.
Using this concept a list with numbers 1 to 5 can be represented as 1:[2,3,4,5].
Using this, let’s try to understand the standard functions in page 6 of the structural induction slides
length [] = 0 -- ( L1 )
length ( x : xs ) = 1 + length xs -- ( L2 )
We can convert this to a mathematical function, since we have multiple lines defining the function this would map to a piecewise function bellow:
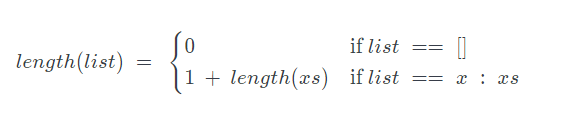
In other words, what this says is if the list is empty then the length of the list is zero. If that’s not the case we learnt above that any non-empty list can be represented in the form of an element concatenated onto another list hence we can write the list as x:xs. If that is the case then the length of the list is 1+ the length of rest of the list xs .
Feel free to skip to the next function if you understood what happens in the above function, but let me show how this function works with an example, lets say we want to calculate the length of the list [1,2] .
When we call length [1,2], Haskell first checks if it is of the form length [] which it is not because the list is not empty. So it then tries to see whether it is of the form length x:xs, where x is 1 and xs is [2] (pattern matching). As this is the case, length [1,2] becomes 1+ length [2] then repeating the above process, we know the list is not yet empty, so it takes the form x:xs where x=2 and xs = [] because of this 1+ length [2] becomes 1 + 1 + length [] now when length [] is called Haskell identifies that the list is empty and returns 0, putting it all together we get:
length [1,2] = 1+ length[2] = 1+ 1 + length [] = 1+ 1+ 0
which is then evaluated to 2, which we know is correct as [1,2] is a list with two elements.
The same concept is used whenever coding with lists, first the function is defined for an empty list, and then for a list with one or more elements.
Looking at the other functions defined on the same page:
map f [] = [] -- ( M1 )
map f ( x : xs ) = f x : map f xs -- ( M2 )
The code above defines function map which takes in a function and a list as inputs. Conceptually map applies the function f to all the elements of the input list.
Similar to the above instance, we start off by defining this for an empty list, which would return an empty list, as there are no elements to apply the function to.
Then the function is defined for the case when the list is not empty, what the second line of the code is saying is
if a function f and a list x:xs are given to the function map, then we apply the function f to x and continue applying the function f to the rest of the list by calling the function with the same input function and the rest of the list.
Let’s see how the above code would work by looking at how map (*2) [1,2] would run:
map (*2) [1,2] = (*2) 1 : map [2] = (*2) 1 : (*2) 2 : [] = 2:4:[] = [2,4]
because the input function was *2 (multiplication by two) each step will apply *2 to the first element of the list till the list is empty.
[] ++ ys = ys -- ( A1 )
( x : xs ) ++ ys = x : ( xs ++ ys ) -- ( A2 )
Here the function ++ is defined, note how it is written in between two inputs, this is called infix notation please feel free to interpret the above as:
(++) [] ys = ys -- ( A1 )
(++) ( x : xs ) ys = x : (++) xs ys -- ( A2 )
Using what you’ve learnt above, try to understand the above function on your own before reading the explanation below. I’ll give you a hint to help, the function takes two lists as input.
So the above two lines of code can be interpreted as as :
- If the first list is empty then the output is just the second list
- If not then the output is the first element of the first list added onto the result of
(++) xs ys
Conceptually the above function will concaternate the first list passed as an argument to the second list. The breakdown of how the output for (++) [1,2,3] [4,5,6] is generated is below:
(++) [1,2,3] [4,5,6] = 1: (++) [2,3] [4,5,6]= 1:2: (++) [3] [4,5,6] = 1:2:3:(++) [] [4,5,6] = 1:2:3:[4,5,6] = [1,2,3,4,5,6]
Trees#
Trees are another recursive data type in Haskell, this has the same structure as a tree in general computer science. Please refer here if you haven’t come across the data type trees.
A tree, can either be empty (an empty tree is called a Null tree) or it can be a Nodewith a tree on the left (called it’s left subtree) and a tree on its right (called the right subtree).
The same thing can be written in Haskell as:
data Tree a = Nul | Node (Tree a) a (Tree a)
In the same manner as lists, any tree that is not null can be denoted in the form Node (Tree a) a (Tree a). Let’s see what trees of different sizes look like in the above format ,
-
Tree with a single node:
Node Nul x Nulwhere x is the node. Graphically this tree would look like: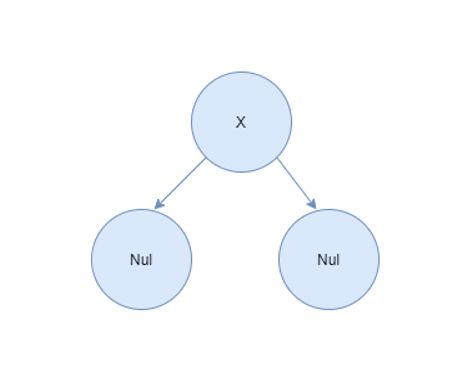
-
Similarly a tree with two nodes can either be written as:
a.
Node (Node Nul y Nul ) x Nulwhich looks like :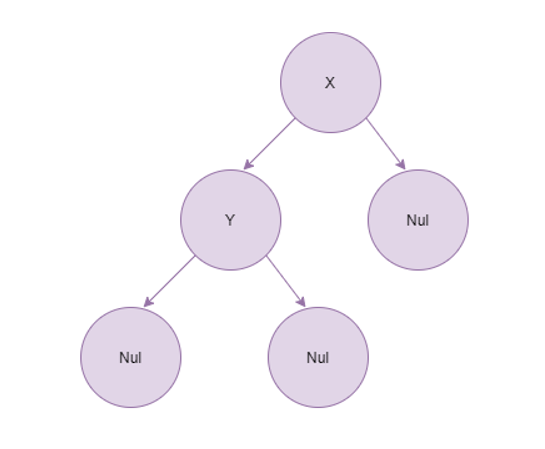
b.
Node Nul x (Node Nul y Nul)which looks like: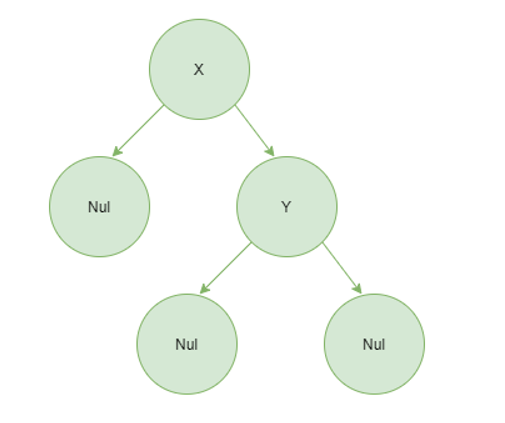
depending on the structure of the tree. Part (a) has the second node as the left subtree, while part (b) has the second node as the right subtree. Likewise, any tree can be written in this form.
Similar to lists, Tree is also a recursive data type. But this time the recursion happens twice with both a left and right subtree. let’s try to understand the basic functions for trees given on page 23 of the week 4 lecture slides.
mapT f Nul = Nul -- ( M1 )
mapT f ( Node t1 x t2 ) = Node ( mapT f t1 ) ( f x ) ( mapT f t2 ) -- ( M2 )
Similar to the map defined for lists, mapT takes in a function and a tree as input and applies that function to every node of the tree, and returns that tree.
Just like how we did it with lists, first the function is defined for a base case. For a list this was the empty list, and for a tree this is a null tree. So the first line of code says that if a null tree is given as input the output would also be a null tree. The second line of code defines the function for any other case. It says that the output is a tree, where the new node is the function applied on the previous node. The subtrees of the output tree, would be the result of using mapT f on each of the input subtrees.
The function below counts all the nodes (that aren’t nul) in the tree.
count Nul = 0 -- ( C1 )
count ( Node t1 x t2 )= 1 + count t1 + count t2 -- ( C2 )
So it defines the base case for when the tree is nul, C1 says that if the tree is nul the output of the count is 0 ( that is a nul tree has no nodes). If that is not the case, the tree can be represented in the form ( Node t1 x t2 ) as mentioned before. Then we know that the tree is not nul, therefore we know the count should be 1+ the number of nodes in both the left and the right subtrees. Which is shown in the second line.
Let’s work through the Haskell code given in the practicals. ( I strongly recommend you trying to understand each bit of code before reading the explanation given.) There were no Haskell code in the first and second practicals. Hence, we start of with practical 3: In this practical sheet there is only one function defined:
sumeven 0 = 0 -- SE1
sumeven n = 2 * n + sumeven (n-1) -- SE2
So first thing to note here is that the function deals with natural numbers and not lists or trees. The first line of the code tells you that if the function was given a single input of value 0, then the output would be 0. But if sumeven was given any other number the output would be 2 times that number plus the output of sumeven run on n-1.
Moving on to practical 4, this sheet has a lot of Haskell functions. Let’s start working through all of them, starting from the appendix.
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys -- A1
(x:xs) ++ ys = x : (xs ++ ys) -- A2
This function was discussed earlier but without the type signature. So the first line says that (++) is a function that takes two lists of a and returns a list of elements of type a. Recall how Haskell functions return a single value. Note how here we use a to denote an arbitrary type, for example if we call (++) [1,2,3] [4,5] then, for this instance, the type signature of the function becomes (++) :: [Int]->[Int]->[Int]. Likewise, the type of a will change each time the function is called. So the type signature of the function can be read as (++) is a function that takes two lists of some type as input and returns a list of that same type as output
the function elem takes a value and a list, and checks if that value is in the list. In other words it checks whether the first argument is an element of the second.
elem :: Eq a => a -> [a] -> Bool
elem y [] = False -- E1
elem y (x:xs)
| x == y = True -- E2
| otherwise = elem y xs -- E3
Notice how the type signature has the term Eq a and it is sperated from the rest by an => instead of a ->. This is not an input to the function, but instead it says that equivalence must be defined for the type a. In other words, Eq a is needed to ensure that the element passes as an argument and the list passed as the second argument can be compared. Eq a is a class defining equals and not equals.
Now here we are dealing with something a little more challenging. The | symbol is used to denote a guard. A guard checks a boolean condition and only executes if the given value satisfies that boolean expression.
Let’s work through the code above, the first line says if the list is empty then the output is false i.e. the element is not in the list (E2). If that isn’t the case we know that the list can be represented in the form x:xs. But now whether or not y is in the list depends on the value of x, for instance if y is equal to x (denoted by y==x) we know the output should be true (E3). If not we should check whether y is in the rest of the list.
This is what the lines below say
elem y (x:xs)
| x == y = True -- E2
| otherwise = elem y xs -- E3
The lines E2 and E3 are called guards. In each of these lines the left hand side of the = sign denote the boolean condition. For line E2, x == y denotes the boolean condition, Haskell executes the code to the right of the = sign if x is equal to y. Otherwise (if none of the boolean statements above are satisfied) then return elem y xs.
(||) :: Bool -> Bool -> Bool
True || _ = True -- O1
False || x = x -- O2
Just like for the (++) in lines O1 and O2 they have used infix notation, and the function can be read as
(||) :: Bool -> Bool -> Bool
(||) True _ = True -- O1
(||) False x = x -- O2
Let’s start off with the type signature, (||) (this is the function OR in Haskell). It takes two booleans and returns a boolean (booleans in Haskell are called Bool). The first line of code used a _, this can be considered as a wild card and can be used to denote anything!! For example, the first line of code will be executed regardless of what the second input is. The first line of code can be read as “if the first input is true return true”, here we don’t consider the second variable at all. The second line can be read as “if the first argument is False, then return the second argument”.
reverse :: [a] -> [a]
reverse [] = [] -- R1
reverse (x:xs) = reverse xs ++ [x] -- R2
Using the type signature it is clear that reverse is a function that takes in a list of some type and returns a list of the same type. Conceptually the function reverses the list, for example if [1,2,3] was given as input the function would return [3,2,1] as output.
This is just like the other functions we saw when we introduced lists. The first line of the code says, if the input is an empty list then return an empty list. If not then add the first element to the end of the reverse of the rest of the list.
Let’s see what happens when we call reverse [1,2,3]:
reverse [1,2,3] = (reverse [2,3] ) ++ [1] = reverse [3] ++ [2] ++ [1] = reverse [] ++[3] ++[2] ++[1] = [] ++ [3] ++[2] ++[1] = [3,2,1]
map :: (a -> b) -> [a] -> [b]
map f [] = [] -- M1
map f (x:xs) = (f x):(map f xs) -- M2
This is the same function that was shown in lectures. We have discussed this above. (Before looking back at the explanation of the function try see whether you can figure it out on your own.)
pref :: a -> [a] -> [a]
pref x l = x:l -- P
pref is a function that takes in a value and a list and adds the value to the start of the list (prepend it). This is what the : does. For example 1:[] = [1].
Now that we understand the code in the appendix, let’s try to work through the code given in the exercises:
size :: Tree a -> Int
size Nul = 0 -- C1
size (Node l x r) = 1 + size l + size r -- C2
This function was covered above.
mirror :: Tree a -> Tree a
mirror Nul = Nul -- M1
mirror (Node l x r) = Node (mirror r) x (mirror l) -- M2
Conceptually what the mirror function does is shown in the diagram below:

Let’s try reading the code, the first line tells us the type signature of the function. The function takes in a tree of type a and returns a tree of type a. The second line of the code says, if the input tree is nul return nul. If not (M2) then the tree can be written in the form Node l x r then we keep x as it is and replace the left subtree with the mirror of r, and replace the right subtree with the mirror of l.
euclid :: Int -> Int -> Int
euclid n 0 = n
euclid 0 m = m
euclid n m = euclid (max n m - min n m) (min n m)
Using the type signature we can see that the function euclid takes two Ints as input and returns an Int. Let’s go line by line from there:
- Line 2: if the second input is 0, then return the first input
- Line 3: If the first input is 0, then return the second.
- Otherwise call
euclidwith arguments(max n m - min n m)and(min n m)
max and min are predefined functions that returns the maximun and the minimun of two numbers respectively.
You don’t have to have use the same words to express what the function does. This is just to help you understand the notation, and help you get the intuition behind the code.
slinky :: [a] -> [a] -> [a]
slinky [] ys = ys -- S1
slinky (x:xs) ys = slinky xs (x:ys) -- S2
slinky is a function that takes in two lists of type a and returns a list of type a. If slinky is given an empty list as its first argument it would return the second argument, if not then it is of the form x:xs. It would call slinky again with the xs as the first argument and x:ys as the second.
rev_a [] ys = ys -- RA1
rev_a (x:xs) ys = rev_a xs (x:ys) -- RA2
rev2 xs = rev_a xs [] -- RR
Here these two functions work together, when rev2 is given a list, it will call rev_a with that same list and an empty list as its second argument.
Looking at the definition of rev_a :
- the first line says, if the first argument is an empty list then return the second list
- If the first list is not empty, then prepend the first element of the first list to the second and call the function again.
Conceptually this does the same thing as reversing a list. Let’s look at what happens when rev_2 [1,2,3] is called
rev_2 [1,2,3] = rev_a [1,2,3] [] = rev_a [2,3] 1:[] = rev_a [3] 2:1:[] = rev_a [] 3:2:1:[] = [3,2,1].
Written by Pramo.